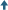The difference between concentration and dose

 Editor’s Note:  The following is freely adapted from “The  Basics of Regulatory Toxicology: Protecting the Public from Harmful Substances,” by  Paul Connett.  Dr. Connett’s article addresses specifically the addition of fluoride to drinking water, but the information he presents can be generalized to apply to any toxic substance that is either accidentally or purposely added to drinking water. It should be obvious to anyone who considers the complexity of attempting to medicate the public by adding chemicals to water that adding a potent poison like fluoride to a public water supply isn’t quite the same thing as adding iodine to table salt. — Hardly Waite.

Concentration is measured in milligrams (mg) of fluoride per liter (1 mg/liter = 1 part per million or ppm). This can be controlled at the water works. Dose is measured in mg/day and this cannot be controlled as it depends on how much someone drinks – and some drink a lot – and how much fluoride they are getting from other sources. It is the total dose that has the potential to harm someone. The concentration (mg/liter) offers no guarantee of safety.

The difference between dose and dosage

The same dose (mg/day) can have different affects on different people. There are two reasons for this:

1) because in a large population there is a large range of sensitivity to any toxic substance,  and

2) because the same dose can have a very different affect on people of different bodyweights.  This is especially relevant when comparing the impacts of the same dose on adults and infants. That is why toxicologists use a different measure called dosage. In this they take account of bodyweight by dividing the dose in mg/day by the adult’s average bodyweight of 70 kg.

Thus supposing it was determined that 7 mg/day was safe for an adult (for some health end point), then the safe dosage (sometimes referred to as a safe reference dose) which can be applied to anyone of any weight including an infant, would be 0.1 mg/kg bodyweight per day.  (7mg/day divided by 70 kg = 0.1 mg/kg/day.)

From a safe dosage we can work out a safe dose for any age range by multiplying the safe dosage by the average bodyweight for that age range. Thus for a 7 kg infant the safe dose for this hypothetical situation would be 0.7 mg/day and for a 20 kg child it would be 2 mg/day.

Going back to the real world. The (EPA) determined a safe reference dosage (for the end point of moderate dental fluorosis) of 0.06 mg/kg/day (the so-called IRIS reference dose). Using this Iris reference dose we can determine the safe dose for a bottle-fed infant – at least for dental fluorosis. Assuming an average bodyweight of 7 kg, the safe dose would be 7 kg x 0.06 mg/kg/day = 0.42 mg/day.

A 7 kg infant drinking 800 ml of formula per day made up with fluoridated water at 1 ppm, would receive 0.8 liters x 1 mg/liter/ day = 0.8 mg/day. In other words a bottle-fed baby consuming water at 1 ppm fluoride would get about twice the safe dose based upon the EPA’s IRIS safe reference dose.

The Agency for Toxic Substances and Disease Registry’s safe reference dosage for bone

ATSDR’s reference dosage for the end point of bone damage was set at 0.05 mg/kg/day. A 70 kg adult would exceed this safe reference dosage if they ingested more than 3.5 mg/day (0.05 mg/kg/day x 70 kg = 3.5 mg/day). Such an adult could exceed this safe reference dosage by

i) drinking 3.5 liters of water at 1 ppm (3.5 L x 1 mg/Liter/day = 3.5 mg/day)

ii) drinking 2.5 liters of water at 1 ppm and getting 1 mg/day from other sources.

iii) drinking 1.5 liters of water at 1 ppm and getting 2 mg/day from other sources.

A U.S. Department of Health and Human Service’s (DHHS) report from 1991 estimated that the range of exposure of the American adult was 1.6 to 6.6 mg/day from all sources.

The large range of sensitivity to any toxic substance

In any large population we can anticipate a very large range of sensitivity to any toxic substance. Like other human traits such sensitivity follows a normal distribution curve (the famous bell-shaped curve). The average person will have an average response but at the two tails – we will have people who are very sensitive at one end and very resistant at the other. Typically we assume some people are going to be 10 times more sensitive than others. This is then used to generate a safety factor of 10 (sometimes referred to as the intra-species safety factor).

Thus if we find harm in a small human study and wish to determine the level that would protect everyone in a large population from that harm this is what we do. We take the dose, which has been found to cause no harm (the so-called no observable adverse effect level or NOAEL) and divide that dose by 10 to give a safe dose for the most sensitive individual in the population. Frequently we don’t have a NOAEL and so we have to use a LOAEL (the lowest observable adverse effect level) and divide that by 100. Sometimes this process is corrupted and it is the LOAEL not the NOAEL that is divided by 10.

Margin of Safety Analysis

Applying these calculations in a real world situation is called a Margin of Safety Analysis and shockingly it is very seldom considered by people who promote fluoridation. They simply use the very crude and highly misleading approach of comparing the concentration used in the study group with the concentration of the fluoride in the water of the fluoridated population as discussed above.

An example of a Margin of Safety analysis using an IQ study

Here I will attempt a real world calculation for lowered IQ. I will use the study by Xiang et al. 2003 who reported a threshold for lowering of IQ at 1.9 ppm of fluoride in the water.

Our first task is to estimate the dose range this represents for the children in the study – which of course, will depend on how much water they drink and how much they get from other sources. We believe very few of these rural Chinese children use fluoridated toothpaste and thus their daily dose comes largely from the water.

• If they drank 2 liters of water per day at 1.9 mg/liter their daily dose would be (2 L x 1.9 mg/L ) = 3.8 mg/day.

• If they drank 1 liter of water per day their daily dose would be 1.9 mg/day

• If they drank 0.5 liters of water per day their daily dose would be approx 1 mg/day.

In other words a reasonable estimate of the range of dose leading to a lowered IQ was approximately 1- 4 mg/day.

If we treat this as a NOAEL the safe range of doses of fluoride to protect the most sensitive child in a large population would be 0.1 to 0.4 mg/day (1-4 mg/day divided by 10). In other words we wouldn’t want a child in a large population drinking more than 400 ml (0.4 L) of water (0.4 liters/day x 1 mg/liter = 0. 4 mg/day).

If the Xiang’s et al. study is valid a responsible regulatory authority would not allow water fluoridation. Little wonder then that fluoridation promoters are doing everything they can to criticize the methodology of the Xiang et al. study and the methodology of all the other 36 studies (out of 43) that have found a lowering of IQ associated with drinking naturally occurring fluoridated water ranging from 0.9 to 11.5 ppm.

Fourteen of the studies, ten of which were part of the 27 studies reviewed in the meta analysis carried out by the Harvard team (Choi et al., 2012), found a lowering of IQ at or lower than 3 ppm. Using the same calculation as above the lowering of IQ was associated with a range of fluoride from 1.5 – 6 mg/day in these fourteen studies. Thus dividing by the safety margin of 10 a dose estimated to be safe for the most sensitive child in a large population would range from 0.15 to 0.6 mg/day.

Even if we take the highest (i.e. least conservative) estimate, such a dose would be exceeded by a child drinking about two large glasses of 1 ppm fluoridated water per day (it could be worse than that because I am using these doses as NOAELs and not LOAELs).

US EPA Office of Water is Not Doing its job.

Using a large amount of taxpayers’ money the US EPA paid the NRC to do the review of their safe drinking water standards discussed above. When the NRC panel released its report in March 2006 it concluded that the EPA’s current safe drinking water standard of 4 ppm (both the MCL and the MCLG are set at 4 ppm) were not protective of health. The panel recommended that the EPA Office of Water perform a new risk assessment and determine a new safe MCLG (maximum contaminant level goal).

The difference between an MCL and an MCLG

The MCL (or maximum contaminant level) for the contaminant in question is a federally enforceable standard and for fluoride it was set at 4 ppm in 1986 by the EPA Office of Water.

The MCLG (or maximum contaminant level goal) is a goal based upon the best science as far as determining harm is concerned with a margin of safety analysis applied sufficient “to protect the most vulnerable from known and reasonably anticipated health effects.” As the name suggests this is not a standard but an ideal goal. Incredibly this was also set at 4 ppm for fluoride in 1986.

What frequently happens for naturally occurring contaminants (e.g. arsenic) is that the economic costs of removing the contaminant to the desired goal (i.e. MCLG) is prohibitively expensive and so a compromise is set between the ideal goal and what can be achieved economically. It is this compromise level, which is the MCL. For arsenic – because it is a known human carcinogen – the MCLG is set at 0. The MCL is set at 10 parts per billion (ppb).

The EPA has not determined a new MCLG after 7 years

It is extremely disturbing that after nearly 7 years the EPA’s Office of Water has not completed the needed risk assessment to determine a new MCLG.

Had the EPA used any one of several end points finding harm in the NRC (2006) review (but particularly the IQ studies) and performed an appropriate margin of safety analysis as discussed above a new MCLG would have to be set well below 1 ppm and thus end water fluoridation immediately. However, it may be that the EPA’s Office of Water is not anxious to remove the rug from under the program that the DHHS (or its preceding agencies) have championed for over 68 years.

Going from a safe reference dose to an MCLG for fluoride

Once one has determined a safe dose sufficient to protect for the full range of sensitivity in a large population the following steps are needed to determine a safe drinking water standard or in this case the MCLG (the maximum contaminant level goal).

We will use another real world example. As explained above using the 14 IQ studies that found a lowering of IQ at 3 ppm or lower a conservative safe dose would be 0.6 mg/day (actually more conservatively it would be 0.15 mg/day).

Now we would have to subtract from this the dose ingested from other fluoride sources. For many children this would be well over 0.6 mg/day (from swallowing toothpaste and food sources). Thus the regulatory agency would have to conclude that given current exposures to fluoride no extra fluoride could be condoned. Thus the MCLG would have to be set at ZERO ppm (like arsenic and lead) – and that dear readers would be the end, finito, morte for water fluoridation!*

This looks like a clear example of bad politics keeping fluoridation afloat. If you can follow the above arguments you will understand this and be in a better position to argue the case.

Given a fair hearing, an application of honest and standard risk assessment procedures and an open-minded judge fluoridation would be over. It is a matter of simple arithmetic and scientific integrity. There’s the rub. Between that arithmetic and this result are powerful political forces who – for reasons I for one cannot fathom – feel the need to keep this practice alive at any cost. That cost today probably includes the lowering of the IQ of our children.

The shift in IQ maybe small, but as Philippe Grandjean (one of the authors of the Harvard meta-analysis by Choi et al, 2012) in his new book (Only Once Chance) explains, a small shift in IQ in the whole population is incredibly serious. For example, a negative shift of 5 IQ points would halve the number of geniuses in our society and double the number of mentally handicapped.

*Completing the MCLG calculation

Had the number after subtraction of other sources of fluoride from the safe dose yielded a number greater than zero then a MCLG would be determined on the basis of an estimate of how much water people drink per day. Typically the EPA assumes that the average person drinks 2 liters of water per day. However, this assumption does not protect a higher-than-average water drinker. Thus at this point the EPA would have to determine what percentage of the population it wishes to protect.

In the 1986 derivation of the MCLG the EPA derived a safe dose of 8mg/day. Then ignoring other sources of fluoride, they assumed an average water consumption was 2 liters per day and thus declared that 4 mg/liter was a safe level. i.e. if someone drank two liters of water at 4 ppm per day they would get 8 mg/day, 2 L/day x 4mg/L = 8 mg / day.